| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Big-Oh
- Java 기초
- 자바 기초
- 이진탐색알고리즘
- Spring 기초
- 순차탐색알고리즘
- 알고리즘 기초
- 평균적인 경우
- 자료구조 기초
- 자바 스캐너
- 평균의경우
- Java
- java기초
- 인프런 스프링
- 코딩테스트
- 코딩테스트 기초
- 자바
- 인프런 자바강의
- 알고리즘
- 윤성우의 열혈구조
- 윤성우의 열혈 자료구조
- 빅-오
- c언어
- 개발 기초
- 프로그래밍 기초
- 시간복잡도
- 백기선
- eclipse 스프링
- 자료구조
- 프로그래밍
- Today
- Total
IT : 기초라는 뿌리
빅-오 표기법(Big-oh Notation) 본문
출처 : 윤성우의 열혈 자료구조
빅-오 표기법(Big-oh Notation)
데이터의 수 n과 그에 따른 시간 복잡도 함수 T(n)을 정확히 그리고 오차 없이 구하는 것은 대부분의 경우 쉽지 않다. 따라서 오차를 허용하지 않으면 ‘+1을 넣는게 맞다 아니다’로 투닥일 것이다.
ex) T(n) = 2n + 1.234..... 이다!!!
하지만 여기서 중점적인 한마디는 그냥 “빅-오만 따지자“ 이다.
도대체 이 빅-오(Big-oh Notation)란 무엇인가?
- O가 매우 크다? 사실상 맞다고 한다. 빅-오라는 것은 함수 T(n)에서 가장 영향력이 큰 부분이 어딘가를 따지는 것인데, 이때 사용되는 표기법에 대문자 O 즉, 큰 O를 사용하기 때문에 빅-오라고 한다.
설명을 위한 함수식
기본 함수 형태
수학적으로 표현한 근사치 식을 구성한다.이렇게 +1쯤은 생략할 수가 있다. 그렇다면 아래와 같이 한차례 간략화를 진행해도 될까?
이 수식에서 2n을 빼도 되는 것이 맞나?라는 생각도 들 수 있을 것이다.


단순하게 빅-오 구하기
자 이제 수식을 보고 빅-오를 구하는 방법은 무엇일까? 수학적인 접근 없이도 다음 사실을 알면 어렵지 않게 빅-오를 구할 수 있다.
T(n)이 다항식으로 표현이 된 경우, 최고차항의 차수가 빅-오가 된다.“
예를 들면 다음과 같다.

그리고 이를 일반화하면 아래와 같게 된다.


하지만 빅-오는 “데이터의 수가 증가에 따른 연산횟수의 증가 형태(패턴)”을 나타내는 표기법이다. 즉, 빅-오의 관점에서 다음 둘은 동일하다.
- 데이터의 수가 2, 3, 4개로 늘어날 때 연산횟수는 4, 8, 16으로 두 배씩 늘어났다.
- 데이터의 수가 2, 3, 4개로 늘어날 때 연산횟수는 99, 198, 396으로 두 배씩 늘어났다.
따라서 다음이 의미하는 바는 O(log n) 과 같이 이해해야 옳다.
“ 데이터 수의 증가에 따른 연산횟수의 증가 형태를 좌표평면상에 그려놓으면, 증가하는 추세는 둔화되는 형태를 띤다. 다시 말해 로그 그래프와 유사한 형태를 띄우게 된다. ”
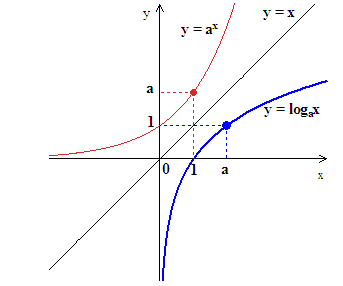
빅오는 성능 분석에 좋은 도구가 된다.
대표적인 빅-오
빅-오 : 데이터 수의 증가에 따른 연산횟수의 증가 형태를 표현한 것.
O(1) : 상수형 빅-오
- 데이터 수에 상관없이 연산횟수가 고정인 유형의 알고리즘을 뜻한다.
- 연산의 횟수가 데이터 수에 상관없이 3회 진행되는 알고리즘일지라도 O(3)이 아닌 O(1)이라고 한다.
- O(1)은 연산횟수가 고정인 유형의 알고리즘을 대표한다는 의미도 있다.
O(log n) : 로그형 빅-오
- 데이터 수의 증가율에 비해 연산횟수의 증가율이 훨씬 낮은 알고리즘을 의미한다.
- 매우 바람직한 유형
- 로그의 밑이 얼마냐에 따라서 차이가 나긴 하지만, 그 차이는 알고리즘의 성능관점에서 매우 미미함.
O(n) : 선형 빅-오
- 데이터의 수와 연산횟수가 비례하는 알고리즘을 의미함.
O(nlog n) : 선형로그형 빅-오
- 데이터의 수가 두 배로 늘 때, 연산횟수는 두 배를 조금 넘게 증가하는 알고리즘을 의미함.
- n과 logn을 곱한 형태라 난해해 보이지만, 알고리즘 중에는 이에 해당하는 알고리즘이 적지 않다.

또한, 빅-오 표기들의 성능(수행시간, 연산횟수)의 대소를 정리하면 다음과 같다.

그래프

'자료구조' 카테고리의 다른 글
| 이진 탐색 알고리즘(Binary Search) - 2(시간복잡도) (0) | 2021.08.12 |
|---|---|
| 이진 탐색 알고리즘(Binary Search) - 1 (0) | 2021.07.26 |
| 순차탐색 알고리즘 시간복잡도 평균적인 경우(Average case) (0) | 2021.07.26 |
| 순차탐색 알고리즘과 시간 복잡도 분석의 핵심요소 (0) | 2021.07.22 |
| 자료구조란 (4) | 2021.07.22 |







